
Torque Formula: Definition and Evaluation Using Real-Time Instances
Whenever you push or pull anything, it requires force to move it from its required place. On the other hand, Torque is commonly known as the rotational or linear movement that acts as a measure of twisting and rotational force dependent on its fixed axis. It indicates that moving any object in a circular or straight position around its axis will produce Torque. For that reason, the torque formula depends on the force and distance required to create the linear or twisting motion on its axis as it creates the turning effect.
Define Torque
To define it clearly, we can examine different examples that will help you learn torque movement quickly. For instance, whenever you open or close your door, it will always require a considerable amount of force to open or close. However, hinged on its axis allows the circular rotation to happen more smoothly.
The greater the force you apply to the door, the more quickly it will turn around on its axis. That turning force creates the effect of torque movement. Moreover, the body movement in your arm or leg offers a similar activity that enables you to experience a torque effect. At the same time, bones get connected at one axis point, giving motion to other body parts. Another typical example is turning a pencil to sharpen it in a sharpener, turning a doorknob, or turning on the water tap, all of which can cause torque movement around its axis.
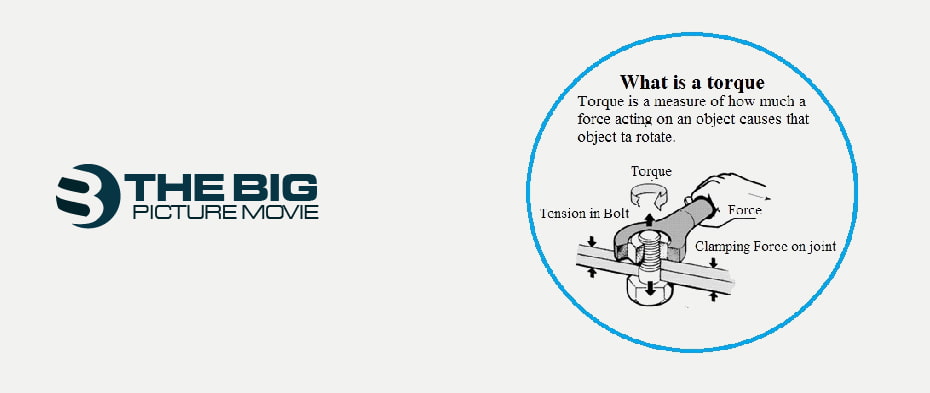
In short, the Torque can be easily defined as: “the turning effect of the force that results in the moment of force.”
Real-world examples for Torque include seesaws and automobile engines, where the twisting force is easily measurable. It helps in creating the rotational movement by revolving on its axis. Similarly, Torque can be one of the determining factors for accessing the vehicle’s strength. Application of Torque in everyday life also includes opening a bottle cap turning the steering wheel, parachute, or pendulum when swinging in the air.
How To Illustrate Torque from Real-Time Instances?
Let us take a cue from its understanding of how torque movement works in the visible evidence in our daily lives. The factor affecting the Torque is, of course, the exerting force. It causes the acceleration of an object either in linear or angular movement. The spanner movement is to tighten or loosen the nuts and bolts. The long arm spanner helps in more effortless rotational motion, whereas the shorter arm spanner restricts the smooth angular movement.

The reason lies in the turning effects of the force exerted on both the spanner instances at different distances with varied angular movement. The moment force for the longer arm spanner is, of course, greater than the shorter arm spanner, despite equivalent force exertion.
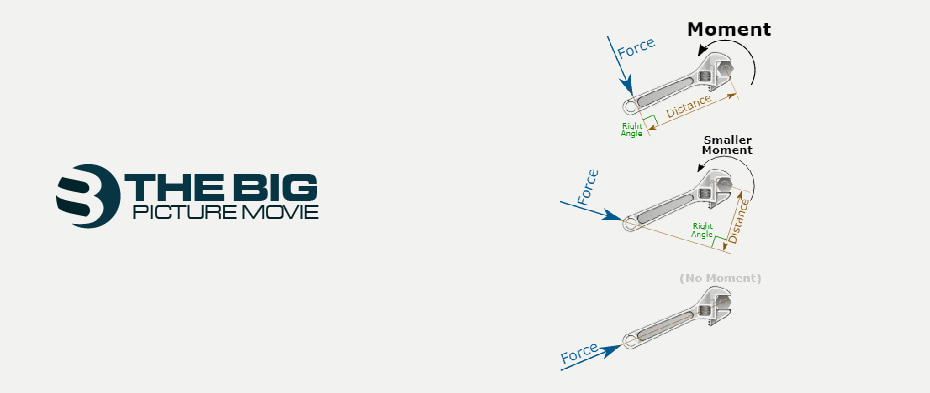
The moment of the spanner remains static when the force makes the right angle with the lever arm. Therefore, you find no moment in the effect of the force applied to it. Moreover, a minor moment results in a shorter distance perpendicular to the force applied to the spanner. The faster and smoother movement takes place at a greater distance perpendicular to the force of the moment arm applied to the spanner. Therefore, the applying force must always be perpendicular to the particular object; otherwise, the force parallel to the object position does not produce Torque.
Type of Torques
Torque can be variable or Static in its mechanism.
Static Torque
Static Torque does not result in any rotational movement. The movement while pushing a closed-door creates the static Torque despite the applied force because it does not make the rotational direction. Furthermore, the constant speed of pedaling bicycle could be another instance whereby you don’t get any acceleration in static Torque.

Dynamic Torque
As for suggesting rotational movement, the driving shaft in the racing car depicts the angular motion. It lets you get the torque movement because it generates a circular motion for your racing car’s wheel. It accelerates your car on the racing track.
In explaining the torque effects, the net force it exerts on an object eventually becomes zero in static movement. That’s the reason why you get the translational equilibrium. On the other hand, the rod tends to rotate; therefore, it produces the turning effect on rotational movement by the force of the moment arm.
Torque Formula with Its Explanation
Let’s see how the torque formula works using a mathematical formula.
Torque = F x L
The Torque mathematically depends on the force (F) and Moment arm (L). The greater the force, the higher the moment arm force (L).
To evaluate the torque magnitude, you first need to calculate the lever arm. Then multiply it by the amount of applied force. To explain it more clearly, it is dependent on the force magnitude. Of course, the distance perpendicular to the Torque is the turning point of effect concerning the forcing points.So, mathematically stating the torque effect, the formula can represent as:
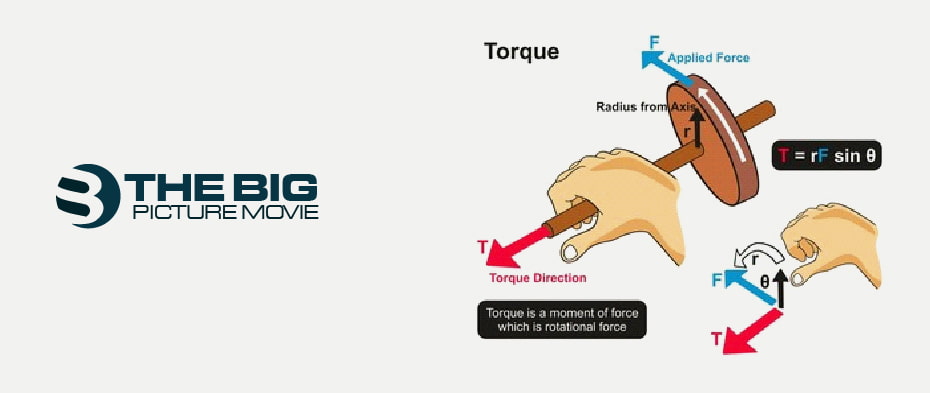
T= f. r sin θ
The magnitude of torque vector (τ) results from the given force (f). Where (r) is the radius of the moment arm and (θ) creates an angle for Force Vector and Moment Arm. In this formula, (r) is the radius for distance covered from its rotation axis due to the applied force in the angular movement.
The Difference Between Torque And Moment Using Its Formula
The difference between Torque and moment seems to be a confusing term used interchangeably. Torque is the particular form of the moment wherein it involves the angular movement around an axis point. However, the moment force results from an external force that helps in angular movement. You can term it a counterpart force that helps in mechanical rotation. The only difference between it and Torque is the ability of the force to generate twist and turning effects around its axis.
The point where the object rotates creates its axis of rotation. The tendency to twist or turn eventually comes from its force. Thus, the force is interchangeably termed as a moment of force.
Evaluate the Torque Formula
To evaluate the torque equation using its simple formula, let’s use the example of a door. It helps to determine the angular moment.
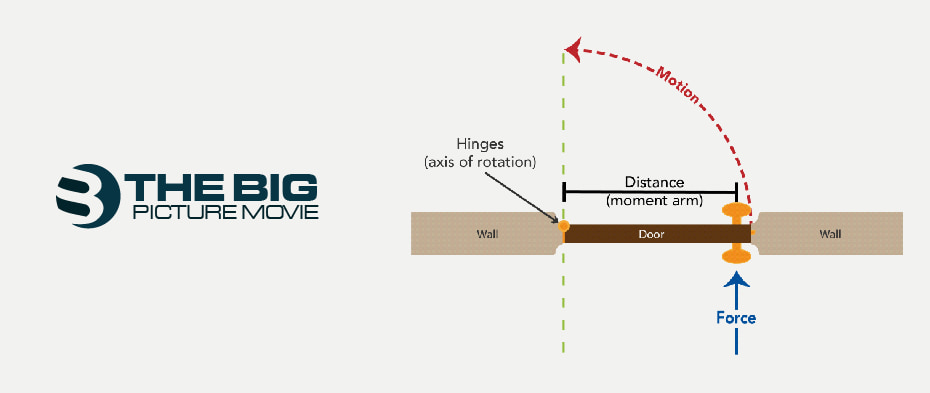
While opening up the door, you apply the force closer to the hinge. It creates more significant pressure for the door’s angular movement. Furthermore, it depends on the direction in which the force is applied. In other cases, if the force is applied perpendicular to the joining axis and line of its moment of force arm, then you will not get the greater force movement. A smaller force moment will be the result of such a movement.
Unit Of Measurement
How can you measure Torque in a unit? It seems to be in combined form, like force and distance it covers using vector position. Its SI measurement unit is the NewtonMeter (N-M). Torque is also a vector quantity since it is a vector product of force and distance. So, with the help of different notations, you can use different torque directions.
That concludes a thorough examination of Torque using real-time cases. I think it will help understand the core notion of Torque and calculate it using its formula.


![MEDDIC [A B2B Sales Methodology]](https://www.thebigpicturemovie.com/wp-content/uploads/2023/01/MEDDIC.jpg)
